Ready to crush the TEAS Math section and secure your spot in nursing school?
You've found the ultimate preparation resource! The ATI TEAS Math Test doesn't have to be the barrier between you and your nursing career. With our expert-designed practice materials and proven strategies, you'll walk into test day with confidence.
Free TEAS Math Sample Questions
Below are some math problems similar to those found on the ATI TEAS Math Test and those found in our Test Prep Pack and our free TEAS Test page. Let's start with three real-world practice questions that reflect what you'll see on the actual exam. Take your time with each one—remember, understanding the process is just as important as getting the right answer.
Numbers and Algebra:
These sample TEAS Math questions primarily assess arithmetic and algebra skills. This question requires arithmetic operations to calculate total points based on given compliments and their corresponding point values.
Question #1 – Problem Solving with Points Calculation
In a TV competition show called "Asgard's got talent" each competitor receives 100 points for every two judges' compliments and 20 points for every 36 family's compliments.
How many points did the competitor "Regina Avalon" obtain if we know she has received 6
compliments from the judges and 12 compliments from each family member?
Additional information- Regina's family is made up of 12 people.
TestPrep-Online Tutor's Tip:
"When I see complex word problems like this, I immediately break them into digestible chunks. Never try to solve everything at once - your brain will thank you!
I always double-check by asking "Does this make sense?" Regina got more judge compliments (which are worth more), so judge points should be higher than family points."
This question involves determining the number of items based on total profit and profit per item, requiring algebraic manipulation.
Question #2 Profit Calculation:
David bought some mouse traps for $800. Later on he sold them for $1240, making $5 on each trap, how many traps were involved?
TestPrep-Online Tutor's Tip:
"I always double-check by asking "Does this make sense?" Regina got more judge compliments (which are worth more), so judge points should be higher than family points.
I always verify my answer: 88 traps × $5 profit = $440 total profit ✓. This quick check catches 90% of calculation errors!"
This question involves calculating fractions of a total and determining the remaining amount, testing arithmetic skills with fractions
Question #3 Fraction of Work Completed:
Of 220 papers that needed to be filed, Brad filed 1/4th and William filed half. How many papers remain that need to be filed?
TestPrep-Online Tutor's Tip:
"Medical conversions are crucial for nursing success! I teach students to master unit conversions because they appear everywhere in healthcare. Here's my foolproof method:
Step 1: Find concentration per 1 mL
- 0.3 mL contains 150 micrograms
- 1 mL contains: 150 ÷ 0.3 = 500 micrograms
Step 2: Convert units
- Remember: 1 mg = 1,000 micrograms
- 500 micrograms = 500 ÷ 1,000 = 0.5 mg
My Success Secret: I always write out the conversion factor: "1 mg = 1,000 mcg" at the top of my scratch paper. This prevents the #1 mistake I see - confusing which direction to convert!"
Math anxiety is common among students. We also offer a Math PrepPack for the HESI 2 which is another nursing entrance exam.
We will continue and tackle a fractions question where we have to convert among fractions, decimals, and percentages:
Question #4 - Fractions
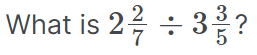
TestPrep-Online Tutor's Tip:
"Outlier questions are my students' favorite once they learn my systematic approach. I always identify the outlier first, then predict the impact.
My method:
Step 1: Identify the outlier
Numbers: 6, 23, 25, 27, 27, 29, 31, 36
6 is clearly the outlier (much lower than the rest)
Step 2: Analyze the median
Original: 8 numbers, median = (27 + 27) ÷ 2 = 27
Without 6: 7 numbers, median = 27 (middle value)
Median stays the same ✓
Step 3: Analyze the mean
Removing a low outlier always increases the mean
We're removing the lowest value, so average goes up ✓
I remember "LOW goes → MEAN grows" and "HIGH goes → MEAN slows." This simple rhyme has helped thousands of my students!"
The skill of converting between fractions and decimals is also useful when you solve difficult calculations. Let's look at a sample question that involves knowing the order of calculation:
Question #5 - Order of Operations
What is
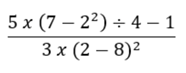
?
TestPrep-Online Tutor's Tip:
"PEMDAS questions make students panic, but I teach a simple approach: "One operation at a time, always!" I never let my students try to do multiple steps mentally - that's where mistakes happen.I write "PEMDAS" at the top of my scratch paper and check off each step. This prevents the #1 mistake - doing operations in the wrong order!"
Boost Your TEAS 7 Math Score
Did you know? Numerical and algebraic questions make over half of the TEAS 7 math section.
Start your focused practice now to:
Solve problems with speed and confidence
Significantly improve your overall score
Ace the TEAS 7 Math: Get Our TEAS Math Pack for Only $59
Question #6-Rounding of Decimals
For the following blood test, you are required to send at least 0.175 liters of blood to the laboratory. Which of the following amounts can be sent:
TestPrep-Online Tutor's Tip:
"I teach the "L to mL rule" - move decimal 3 places RIGHT. And remember: medical minimums are NEVER negotiable - always choose the amount that exceeds requirements!"
Practice identifying decimal places quickly: tenths (1st after decimal), hundredths (2nd), thousandths (3rd), and so on. This skill will help you in many math and science applications. Try our free science test practice and see for yourself.
Master TEAS Math: Your Free Study Guide Awaits!
Now that you've explored the "Numbers and Operations" section, take your TEAS Math prep to the next level. Our comprehensive free study guide covers all essential topics.
Download Your free TEAS 7 Math Study Guide PDF.
Use it with our free TEAS practice test below
Measurement and Data
There are 16 questions in this sub-section - Measurement and Data. Make sure you understand the answers and explanations provided, and use our Study Guide to familiarize yourself with the subtopics:
The following question shows that you can read bar graphs, line graphs, and pie charts.
Question #7 - Reading Data
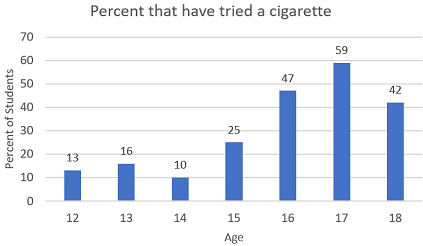
A teacher in school asked students whether they had tried a cigarette or not. The data is displayed in the chart. What is the mean percent of students who have tried a cigarette aged 15 through 18? (Round the answer to the nearest tenth.)
TestPrep-Online Tutor's Tip:
"I always highlight the specific age range in the question. This prevents the most common mistake - including data that shouldn't be there!"
Get Our TEAS Test Pack
Don't miss this opportunity to jumpstart your TEAS 7 prep
A good strategy for analogy questions is to start by making up a short, simple sentence to connect the two words in the first analogy. For example: “A parody is satirical.” Then, you can substitute in the words from the second analogy to help you eliminate answer choices.
Let's move on to the next measurement and data question. This question asks you to identify independent and dependent variables and to distinguish between positive and negative correlations.
Question #8 - Variables Relationships:

Which of the following statements about the table are correct?
TestPrep-Online Tutor's Tip:
"I visualize the graph in my head. If the line goes up from left to right, it's positive. If it goes down, it's negative. Simple as that!"
Moving on to the topic of medication dosages and unit conversions, let's examine a critical scenario involving an allergic reaction and emergency treatment.
Question #9 - Converting between Measurements:
Harriet, who is allergic to peanuts, accidently consumed a small amount of peanut oil while visiting a restaurant. Consequently, she suffered from anaphylactic shock, and was rushed to the nearest hospital, where she was injected with a 150 micrograms/0.3ml adrenaline solution.
How much adrenaline is found in 1 milliliter of the solution?
TestPrep-Online Tutor's Tip:
"Two-step conversion problems are where students make the most mistakes. I teach a simple mantra: "Scale up first, then convert units." Never try to do both steps at once!"
Shifting our focus to everyday medical calculations, we'll now consider a common situation many medical staff face when administering over-the-counter medication to their children.
Question #10 - Basic Arithmetic in a Pratical Setting
Mary wishes to give liquid Tylenol to her two young children (3 and 5 years old), both suffering from fever. According to the label, between the ages of 2–3, the recommended dosage is 5 milliliters, and between the ages of 4–5, the recommended dosage is 7.5 milliliters. For both age groups, a maximum of five doses are allowed per day.
How much liquid Tylenol does Mary have to buy if she wants to be sure she has enough medicine to give both children maximum dosages for four days?
TestPrep-Online Tutor's Tip:
"Multi-variable problems overwhelm students, but I break them down using my "organize first, calculate second" approach. I never let students jump straight into math - organization prevents 80% of errors."
We conclude our free sample TEAS Math questions by asking a question about data.
Question #11 - Data
6, 23, 25, 27, 27, 29, 31, 36
Which of the following conclusions would be correct if the outlier was removed from this set?
TestPrep-Online Tutor's Tip:
"Outlier questions are my students' favorite once they learn my memory trick: "Kill the extreme, boost the mean!" When you remove an extreme low value, the average goes up.
Step 1: Spot the outlier
Data: 6, 23, 25, 27, 27, 29, 31, 36
6 is way lower than the cluster (23-36)
Step 2: Check median impact
Original: 8 numbers, median = (27+27)÷2 = 27
Without 6: 7 numbers, median = 27 (middle value)
Median unchanged ✓
Step 3: Check mean impact
Removing lowest value always increases mean
Think: if you remove the worst grade, your average improves!
I use the phrase "Low goes, mean grows" - it's cheesy but my students never forget it!"
Question #12
A farmer needs to calculate how much feed to buy each week for his farm. He knows that each cow eats 24 pounds of feed a day and each pig eats 7 pounds of feed a day. If he has x cows and y pigs, how much feed does he need to buy each week?
TestPrep-Online Tutor's Tip:
"Word-to-algebra problems scare students, but I teach them to think in steps: "Daily first, then weekly." Never try to jump straight to the final expression - build it piece by piece."
Master Every TEAS Math Challenge
• Conquer Numbers & Operations with crystal-clear examples
• Demolish Algebra problems using proven shortcuts
• Ace Measurements & Data without breaking a sweat
Begin your TEAS test practice now with our most comprehensive preparation pack, the ATI TEAS Premium Pack.
What Is the ATI TEAS Math Test?
The ATI TEAS Math is a section that is found inside the ATI TEAS exam. It is comprised of the following topics:
- Numbers and Algebra (18 items)
- Measurement & Data (16 items)
- Additional 4 pretest items are included that do not count for your final score
You will have 54 minutes to answer the 38 items on the Math section. The use of a calculator in this section is permitted.
We recommend you use our study guide to ensure you cover all sub-topics. You will be given here a few sample questions from each domain, but notice that each domain has the following sub-topics:
- Numbers and Algebra: order of operations, place value, number order, rounding, fractions, decimals, percentages, constant and variables, equations and inequalities, and problem solving.
- Measurement and Data: US standard system of measurement, metric system of measurement, converting between measurements, geometric/physical quantities, reading data, variable relationships, and statistics terms.
ATI TEAS Math FAQ's
The TEAS Math tests practical math skills needed for nursing school success. You'll encounter arithmetic, basic algebra, unit conversions, data interpretation, and statistics. Our prep pack covers every topic with authentic practice questions.
You'll answer 38 questions in 54 minutes. This includes 34 scored questions and 4 pretest questions (which don't count toward your score). Time management is crucial!
Yes! A four-function calculator is provided on-screen. However, don't rely on it completely - practice mental math shortcuts to save time on simple calculations.
Most nursing programs accept scores of 65-70% or higher. Top-tier programs often require 80%+. Our students typically see 15-20 point improvements after using our prep pack.
Most students need 2-4 weeks of focused study. If math isn't your strength, start with 6-8 weeks. Our prep pack includes a customized study schedule based on your target score.
Absolutely! Our questions closely mirror the actual TEAS in difficulty, format, and content.



